(1). Unknown Environment: The exact shape and locations of obstacles must be detected online and coverage path must be adapted in real time based on information derived from sensor measurements.
(2). Path Pattern: The algorithm should produce the desired back-and-forth coverage path, as compared to spiral path that require a high number of turns for the vehicle;
(3). Tasking and Navigation Control for the Autonomous Vehicle: The autonomous vehicle must perform tasks (e.g., cleaning) in the coverage region, hence it must receive tasking and navigation commands from an on-board supervisor.
(4). Computational complexity: The complexity for waypoint computation must be fairly low for suitability to real- time applications.
(5). Complete coverage: The algorithm must not suffer from the looping or the local extrema problem, and it must guarantee complete coverage in finite time.
The ε* (pronounces: epsilon star) Algorithm: We proposed a novel sensor-based coverage path planning algorithm, called ε*, that guarantees complete coverage in unknown environments. The algorithm generates a back-and-forth trajectory with shorter length and less number of turns as compared to a number of popular existing coverage algorithms, as shown on the right hand side. More details are published [here].
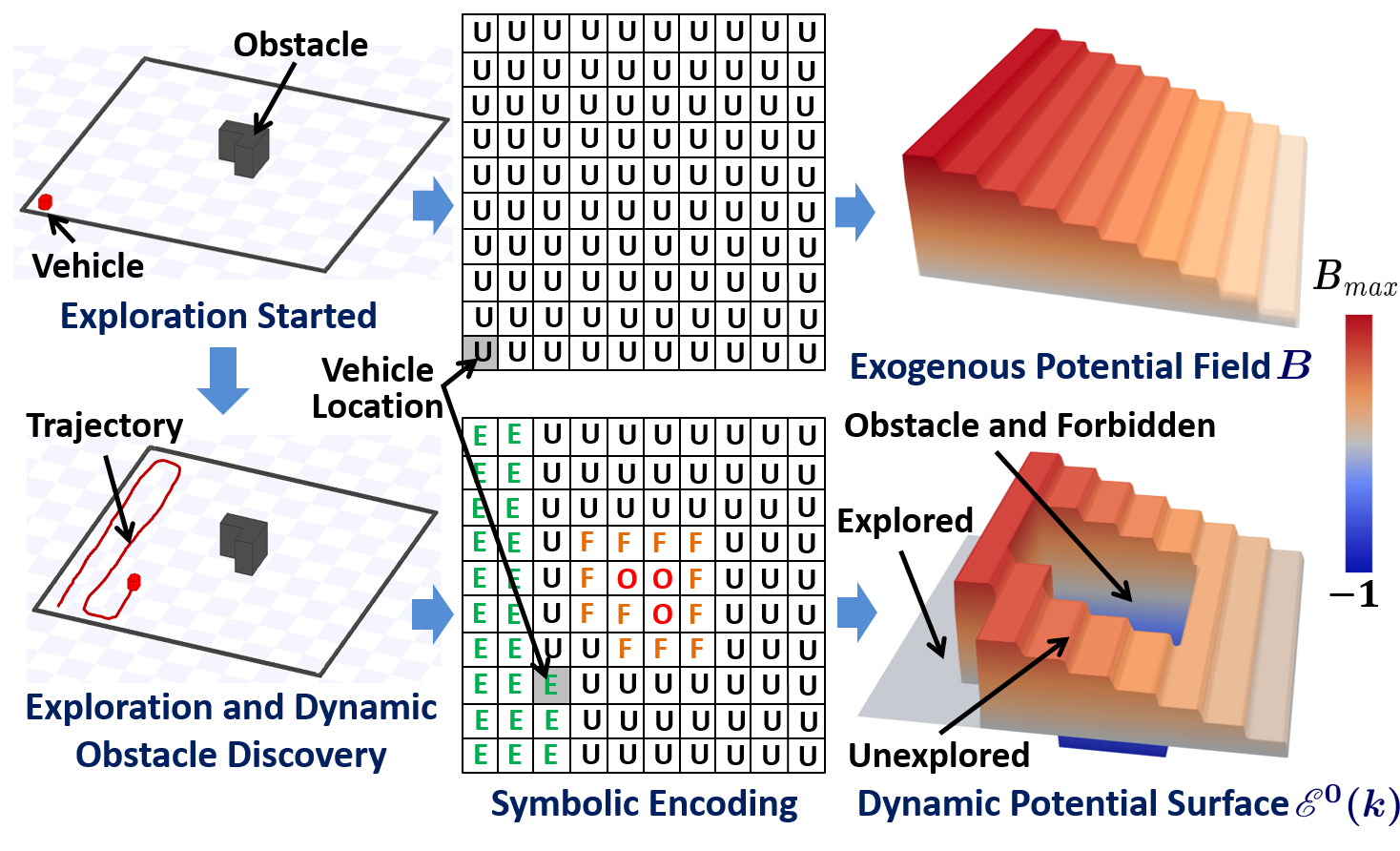
The algorithm utilizes the concept of an Exploratory Turing Machine (ETM), which acts as a supervisor to the autonomous vehicle and guides it with navigational commands.
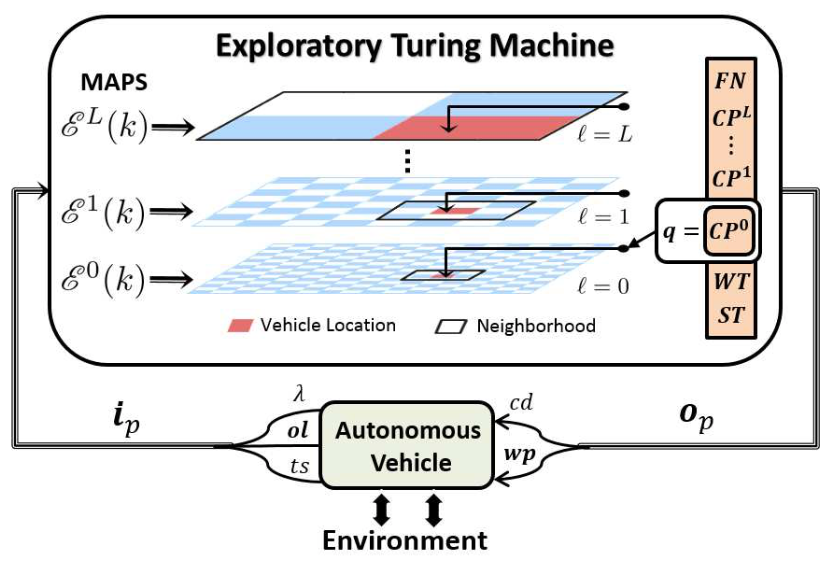
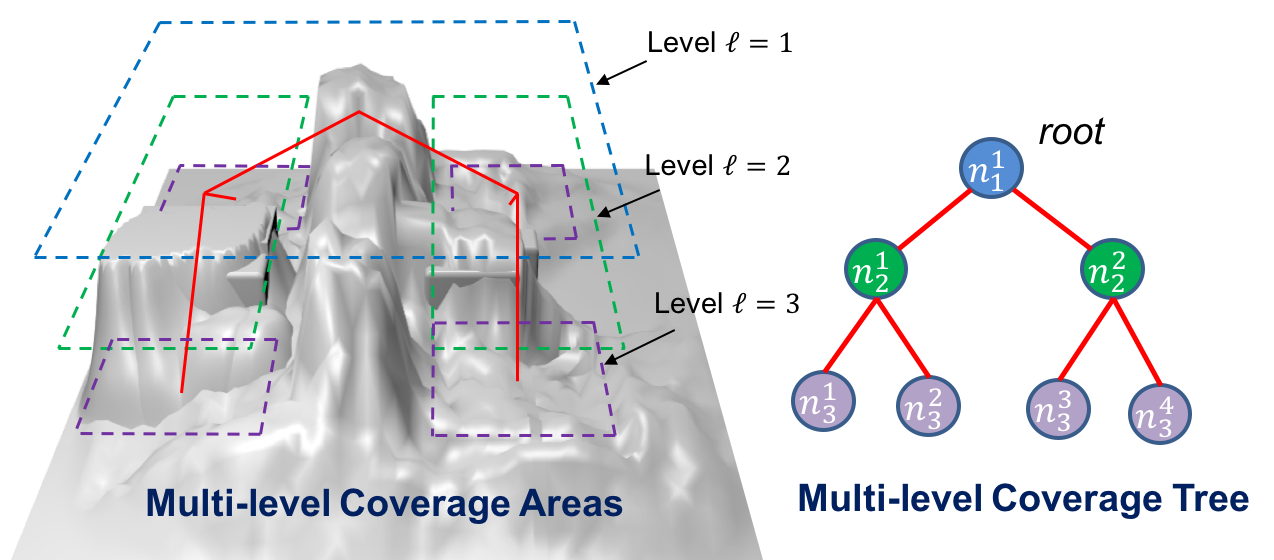
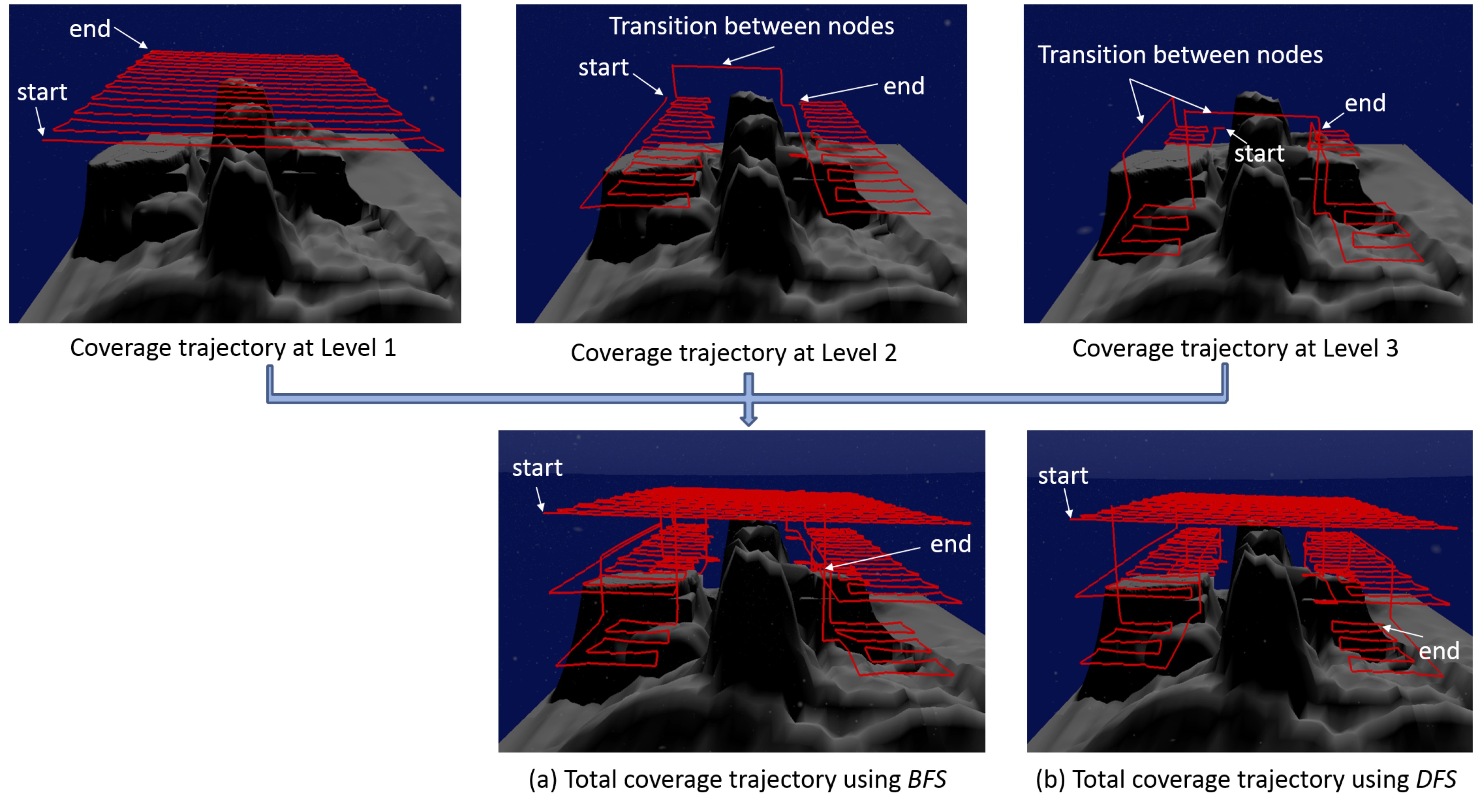
Typical operation of ETM: As an example, as shown below, initially, the entire search area is unknown hence all grid cells at level ℓ = 0 are assigned with symbol "U" (i.e., unexplored) and the potential surface is assigned with a time-invariant exogeneous positive potential field B, which is designed offline to have plateaus of equipotential surfaces along each column of the cells. The plateaus monotonically increase in height by one unit from 1 on the rightmost column to the maximum value on the leftmost column. Thus, such B facilitates the back-and-forth motion in an obstacle free region by following the highest positive equipotential surface from left to right.
Then, as the autonomous vehicle explores the search area and uses its on-board sensing systems to discover explored ("E"), obstacle ("O") and forbidden ("F", i.e., a buffer created around obstacles to prevent collision due to sensor noise) cells, the corresponding potential for explored cells are turned to 0, while the potential for "O" and "F" cells are turned to -1. These assignments will help obstacle avoidance and also prevent the vehicle from re-visiting already tasked cells. The next waypoint is the center of the cell in its neighborhood that has the max potential.
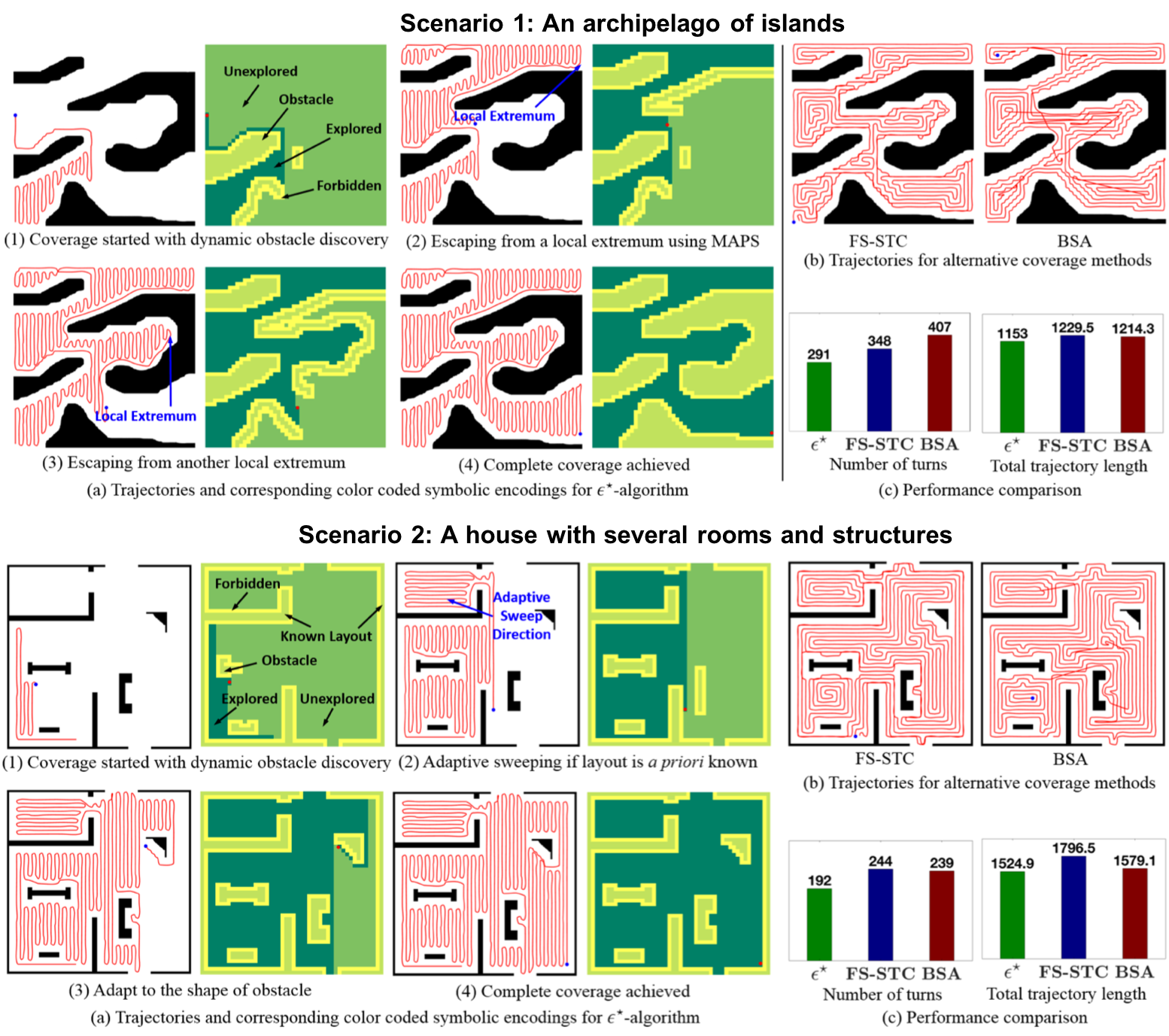
Validations: Simulations on Player/Stage
A comparison of coverage path with alternative online CPP methods in two complex environment
Videos: Simulations on Player/Stage Simulator
Validations: Real Experiments
The algorithm was further validated in real experiments using an autonomous ground vehicle (AGV) that is equipped with a HOKUYO laser, a Hagisonic StarGazer indoor localization system and ten ultrasonic sensors. The videos are show below.
Videos: Real Experiments using an Autonomous Ground Vehicle